A short introduction on Meta-Modelling and Kriging

In many branches of science and particularly Engineering, there are lots of complex physical models that are very hard to evaluate, or in the other hand there might be some data available that there is no physical model to describe them. Regarding to these issues, Surrogate models or Meta-models provide a very appropriate tool to be able to address such problems. Meta-models can replace a very complex mathematical model which is very expensive to evaluate with a simpler model, therefore,  applying available numerical methods on the meta-model will be much cheaper. Also, for those data that there in no model available, one can say that surrogate models are the only remedy. 

Having a good design of experiment is adequate to prepare the meta-mode and this is a great advantage for this approach since design of experiment is a small set of realisations of input variables and the corresponding output of the complex original model. Hence, the effective cost of meta-model goes for the choice of design of experiment. 

There are different types of meta-modelling such as functional basis methods, Gaussian regression and spectral methods. Choosing among these methods depends on the quality of the method and their ability to address high dimensional problems with a good accuracy. 

Gaussian process regression (Kriging) 

Among different methods of meta-modelling Kriging meta-modelling or Gaussian process regression is one of the most interesting methods. Kriging metamodeling has been formulated by a French mathematician George Matheron around 1963 and he named the methodology after a South African mining engineer D. G. Krige who applied this methodology for the first time in geo-statistical problems. In fact, Kriging is the best linear and unbiased prediction of the unknown value of a random function M at any voluntary location. 

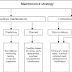
Kriging meta-modelling is based on this idea that any physical model can be formulated by combining a regression model with a stochastic process. By using the design of experiment, regression model tries to find the general trend of the original model and stochastic part reduces the distance of the approximation by regression and the points in design of experiment to zero. Different steps of Kriging is illustrated in Figure 1. 

Kriging meta-models can provide a very helpful tool in the area of structural reliability analysis. There are different methods developed out of kriging for reliability analysis such as EGRA, Independent EGO, Mixed EGO, AK-MCS, etc. ((H. Zhen & D. Xiaoping, 2015), (W. Fauriat & N. Gayton 2013 ), (B. Echard et al. 2011)). 

Figure 1 Kriging modelling steps